Turmas 721 & 722
II UNIDADE
Download da II Avaliação – Turma 721 / Turma 722
Abordagens sobre logarítmos
Download I Avaliação da II Unidade: Turma 721 / Turma 722
Abordagens sobre Funções e Equações Exponenciais
Exercícios de Equações Exponenciais Online – parte I
Exercícios de Equações Exponenciais Online – parte II
MATERIAL DE ESTUDO
Revendo alguns conceitos e tipos de funções
LISTA 4 – Lei dos Senos e Cossenos
I UNIDADE
Download da Avaliação de Recuperação Paralela
Download da 1ª Avaliação: Turma 721 – Turma 722
LISTA 3 – Funções e Equações Trigonométricas
LISTA 2 – Relações Trigonométricas
Gabarito da Lista 2
LISTA 1 – Introdução ao estudo da trigonometria
MATERIAL PARA ESTUDO
1ª AVALIAÇÃO DA TURMA 722: 21/3/11
1ª AVALIAÇÃO DA TURMA 721: 22/3/11
Ementa:
- Trigonometria e Funções Trigonométricas;
- Funções Exponenciais e Logarítmicas;
- Matrizes e Determinantes;
- Sistemas Lineares.

Professor,
Encarecidamente me dê uma ajuda com relação a questão 5 da prova da 721… porque no meu desenvolvimento rendeu até o passo de log x 12 1/3 onde eu sei q posso expandir esse 12 em 3*4 e a partir de então eu não sei mais “caminhar”…
Meus cumprimentos! Boa Noite!
Ananda, como você fez![\log_x \sqrt[3]{12}=\log_x 12^{1/3}](https://s0.wp.com/latex.php?latex=%5Clog_x+%5Csqrt%5B3%5D%7B12%7D%3D%5Clog_x+12%5E%7B1%2F3%7D&bg=ffffff&fg=555555&s=0&c=20201002) . Basta usar a propriedade de logarítmo de uma potência (
. Basta usar a propriedade de logarítmo de uma potência ( ). Assim, tem-se
). Assim, tem-se  . Como você bem citou pode escrever
. Como você bem citou pode escrever  . Assim, você tem
. Assim, você tem ![\log_x \sqrt[3]{12}=\log_x 12^{1/3}=\frac{1}{3}*\log_x 12=\frac{1}{3}*\log_x (3*2^2)=\frac{1}{3}*(\log_x 3 + \log_x 2^2)=\frac{1}{3}*(\log_x 3 + 2*\log_x 2)](https://s0.wp.com/latex.php?latex=%5Clog_x+%5Csqrt%5B3%5D%7B12%7D%3D%5Clog_x+12%5E%7B1%2F3%7D%3D%5Cfrac%7B1%7D%7B3%7D%2A%5Clog_x+12%3D%5Cfrac%7B1%7D%7B3%7D%2A%5Clog_x+%283%2A2%5E2%29%3D%5Cfrac%7B1%7D%7B3%7D%2A%28%5Clog_x+3+%2B+%5Clog_x+2%5E2%29%3D%5Cfrac%7B1%7D%7B3%7D%2A%28%5Clog_x+3+%2B+2%2A%5Clog_x+2%29&bg=ffffff&fg=555555&s=0&c=20201002) . Aqui usamos a propriedade de logarítmo da soma (
. Aqui usamos a propriedade de logarítmo da soma ( ) e novamente a propriedade de logaritmo da potência.
) e novamente a propriedade de logaritmo da potência.
Agora, por último, basta substituir os valores dados.
Professor, tentei resolver a avaliação da 721 e não consegui resolver as questões 1 e 7, há possibilidade do senhor passar a resolução agora, urgente!!
Obrigado.
Thierry, minha internet estava ruim. e assim sucessivamente com as outras potências e depois você pode fazer a substituição
e assim sucessivamente com as outras potências e depois você pode fazer a substituição  . No final você vai ter y no numerado e denominador e pode simplificar, encontrando como resultado 82/3.
. No final você vai ter y no numerado e denominador e pode simplificar, encontrando como resultado 82/3. como
como  e novamente faça a substituição de
e novamente faça a substituição de  .
.
Não se dar um peixe e sim se ensina o homem a pescar. Então vou lhe dar dicas:
Na questão 1 basta aplicar as propriedades de potências: multiplicação de potências de bases iguais e divisão de potências de bases iguais (ambas estudadas na 5ª e 7ª série e revisadas na sala antes de iniciarmos exponencial, dê uma olhada no seu caderno, caso tenha copiado). Assim você deve separar, por exemplo,
Quanto a questão 7, escreva
Olhe os exemplos de substituição que resolvemos em sala.
OBS.: O Murilo e o Bira responderam a questão 5, troque figurinha com eles.
Muito obrigada professor! consegui resolvê-las mais acredito que na segunda-feira pela manhã estarei tirando ainda inúmeras duvidas… tenha um bom dia!
Professor,
fazendo os exercícios de GELSON, Iezzi, há uma questão 143 (f e h) em que expõe respectivamente: 3^2-log3^6 e 9^2-log3^√2. O fato é que isso tem ligação às propriedades de divisão…
mas não consigo expor essa propriedade no problema… Há uma maneira de você me ajudar?
Abraço!
Ananda, a questão não é 143 e sim 144. . Aplicando a propriedade de potência de divisão de bases iguais(“ao contrário”), temos o seguinte:
. Aplicando a propriedade de potência de divisão de bases iguais(“ao contrário”), temos o seguinte:

 .
.

A resolução da letra (f) é análoga a resolução dada na letra (b) da 143.
Na letra (f) temos o seguinte:
Pela 3ª propriedade do livro de Iezzi(na parte superior desta mesma página) e dada em sala de aula
Agora é só finalizar a resolução da questão, não esquecendo de simplificar a resposta,quando possível. No final do livro tem um gabarito.
Para responder a letra (h) siga o mesmo raciocínio da resolução da letra (a) da questão 143.
Usando o referido raciocínio e a propriedade citada na questão anterior, temos
Confira as contas e verifique o gabarito.
Espero te ajudado, para quaisquer dúvidas estarei a disposição. Estarei no IFBA na segunda pela manhã, caso necessite.
Professor, gostaria de saber se por exemplo, se eu quiser apresentar um trabalho na SEEINFO pra Algoritmos, obrigatoriamente ele vai ser avaliado pra Matemática?
Jarbas, depende do tipo de trabalho. Caso vc queira que seja avaliado, terá que me falar sobre sua proposta para eu verificar a viabilidade de avaliá-lo.
Amanhã estarei no IFBA à tarde às 14h. As 16h viajo e só retorno na segunda. Então vc precisa me procurar amanhã no horário indicado.
Sua avaliação está com Nayra(representante da turma).
Professor Valdex..
Você comunicou a turma 722 que gostaria de retorno com relação a quem participaria ou não da Seeinfo…eu portanto, lhe comunico que não participarei e que conseqüentemente a minha avaliação terá que valer o peso 10 proposto em sala… um grande abraço! e bom finds!
Ok, Ananda!
Idem pra ti!!!
“Brigadão” professor!
Ah! E por falar nisso amanhã você estará na Instituição pela manhã? Em quais horários? abraços!!!
Professor:
Montando um grupo de estudo esse final de semana e percebemos que nossas maiores duvidas foram diante das questões 5, 6 e 10… Você poderia desenrolar parte delas pra que possamos compreendê-las?
Desde já agradecemos…
Ananda, segue algumas dicas:
Questão 5: Utilize a fórmula de tangente estudada em sala, a saber: na expressão de y, calcule o mmc no numerador e denominador e faça as divisões de frações correspondentes e ai você encontrará
na expressão de y, calcule o mmc no numerador e denominador e faça as divisões de frações correspondentes e ai você encontrará

 , então eleve a expressão anterior ao quadrado. Assim você terá que desenvolver o produto notável correspondente e usando o fato de que
, então eleve a expressão anterior ao quadrado. Assim você terá que desenvolver o produto notável correspondente e usando o fato de que  (Relação Fundamental) você terá finalmente a expressão
(Relação Fundamental) você terá finalmente a expressão

 . Assim substitua
. Assim substitua  por
por  e, finalmente, você encontrará a solução
e, finalmente, você encontrará a solução 
Como estou pedindo o valor de
Como trabalhado em sala, sabemos que
Questão 6: Utilize a fórmula dada em sala para (também referida na questão anteriormente comentada). Como queremos as raízes para a equação de y, então iguale tal expressão a 0. Então você terá que
(também referida na questão anteriormente comentada). Como queremos as raízes para a equação de y, então iguale tal expressão a 0. Então você terá que  ou
ou  . Analise os possíveis valores de x no intervalo dado.
. Analise os possíveis valores de x no intervalo dado.
Questão 10: Como a função cosseno é par, a funcão secante que é a razão entre 1 e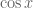 , também é par. Assim
, também é par. Assim  . Utilize este fato e em seguida eleve ambos os lados da equação dada ao quadrado. Resolvendo o produto notável no primeiro membro você encontrará
. Utilize este fato e em seguida eleve ambos os lados da equação dada ao quadrado. Resolvendo o produto notável no primeiro membro você encontrará
 . Substitua a fórmula de secante apenas no termo central e ai você terá
. Substitua a fórmula de secante apenas no termo central e ai você terá  . Finalmente isolando
. Finalmente isolando  temos
temos 
Caso as dúvidas persistam pode me procurar na sala dos professores amanhã pela manhã.
vlw!!!
profº tem com mostrar um caminho para a resolução das questões 2,3,9 e 8 !!!
Questão 2: Observe que falei que e que x é do terceiro quadrante. Sabemos que
e que x é do terceiro quadrante. Sabemos que  tem tangente igual a 1. Assim o ângulo solicitado é um correspondente a
tem tangente igual a 1. Assim o ângulo solicitado é um correspondente a  graus no terceiro quadrante, ou seja,
graus no terceiro quadrante, ou seja,  que se encontra somando
que se encontra somando  a
a  . Agora você já está em condições de analisar as alternativas. Tem duas respostas corretas.
. Agora você já está em condições de analisar as alternativas. Tem duas respostas corretas. trabalhada em sala(olhe no seu caderno). Posteriormente é só analisar qual ângulo no intervalo
trabalhada em sala(olhe no seu caderno). Posteriormente é só analisar qual ângulo no intervalo ![]0,\pi/2[](https://s0.wp.com/latex.php?latex=%5D0%2C%5Cpi%2F2%5B+&bg=ffffff&fg=555555&s=0&c=20201002) satisfaz a resposta encontrada.]
satisfaz a resposta encontrada.] e ai você vai colocar o seno em função do cosseno e então use a fórmula trabalhada em sala para
e ai você vai colocar o seno em função do cosseno e então use a fórmula trabalhada em sala para  e faça a substituição da expressão encontrada para o seno nesta. OBS.: Observe o gabarito.
e faça a substituição da expressão encontrada para o seno nesta. OBS.: Observe o gabarito. e em seguida utilize os valores de seno e cosseno de
e em seguida utilize os valores de seno e cosseno de 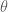 dados.
dados.
Questão 3: Iguale as duas funções, pois elas se inteceptam no mesmo ponto de ordenada y. Então use a fórmula de
Questão 8: Utilize a fórmula de tangente
Questão 9: Utilize as fórmulas da adição de arcos trabalhas em sala para desenvolver a expressão
Espero ter ajudado, bons estudos!!
OBS.: As avaliações serão corrigidas em sala de aula.