Composição de Funções
Sabemos que uma função é uma relação existente entre duas variáveis, onde uma depende do valor da outra, formando assim pares ordenados que podem ser representados no plano cartesiano. Observe alguns exemplos de funções e suas definições:
f(x) = 2x + 1 → note que f leva cada valor de x ao resultado 2x + 1.
g(x) = 2x → note que f leva cada valor de x ao resultado 2x.
Mas, e se quisermos chegar a um determinado resultado aplicando um número real sucessivamente à lei das funções: f e g? Para esse tipo de situação utilizamos as propriedades de uma função composta, nesse caso devemos originar uma nova função, observe: h(x) = g(f(x)), função h é a composta de g com f.
Matematicamente falando, temos que f: A → B e g: B → C, denomina a formação da função composta de g com f, h: A → C. Dizemos função g composta com a função f, representada por gof.
f(x) = 2x + 1 e g(x) = 2x
h(x) = g(f(x))
h(x) = g(2x+1)
h(x) = 2 * (2x+1)
h(x) = 4x + 2
Exemplo 1
Dada as funções f e g de domínio real definidas por f(x) = 3x – 2 e g(x) = – 4x + 1. Determine a lei que define:
a) f(g(x)) → f(– 4x + 1) → 3(– 4x + 1) – 2 → –12x + 3 – 2 → –12x +1
b) g(f(x)) → g(3x – 2) → –4(3x – 2) + 1 → –12x + 8 + 1 → –12x + 9
Exemplo 2
Sejam as funções f(x) = 2x – 6 e g(x) = x + 10, determine o valor de:
a) f(g(2) )→ f(2 + 10) → f(12) → 2*12 – 6 → 24 – 6 → 18
b) f(g(5) → f(5 + 10) →f(15) → 2*15 – 6 → 30 – 6 → 24
c) g(f(–6)) → g(2*(–6) – 6) → g(–12 – 6) → g(–18) → –18 + 10 → –8
d) g(g(3) → g(3 + 10) → g(13) → 13 + 10 → 23
Exemplo3:
Ao considerarmos as funções f(x) = 4x e g(x) = x² + 5, determinaremos:
a) g o f
(g o f)(x) = g(f(x))
g(x) = x² + 5
g(4x) = (4x)² + 5
g(4x) = 16x² + 5
(g o f)(x) = g(f(x)) = 16x² + 5
b) f o g
(f o g)(x) = f(g(x))
f(x) = 4x
f(x² + 5) = 4 * (x² + 5)
f(x² + 5) = 4x² + 20
(f o g)(x) = f(g(x)) = 4x² + 20
Exemplo 4:
Vamos determinar g(f(x)) e f(g(x)), em relação às funções f(x) = x + 2 e g(x) = 4x² – 1.
(g o f)(x) = g(f(x))
g(x) = 4x² – 1
g(x + 2) = 4 * (x + 2)² – 1
g(x + 2) = 4 * (x + 2) * (x + 2) – 1
g(x + 2) = 4 * (x² + 2x + 2x + 4) – 1
g(x + 2) = 4 * (x² + 4x + 4) – 1
g(x + 2) = 4x² + 16x + 16 – 1
g(x + 2) = 4x² + 16x + 15
(g o f)(x) = g(f(x)) = 4x² + 16x + 15
(f o g)(x) = f(g(x))
f(x) = x + 2
f(4x² – 1) = (4x² – 1) + 2
f(4x² – 1) = 4x² – 1 + 2
f(4x² – 1) = 4x² + 1
(f o g)(x) = f(g(x)) = 4x² + 1
Representação esquematizada de funções compostas:
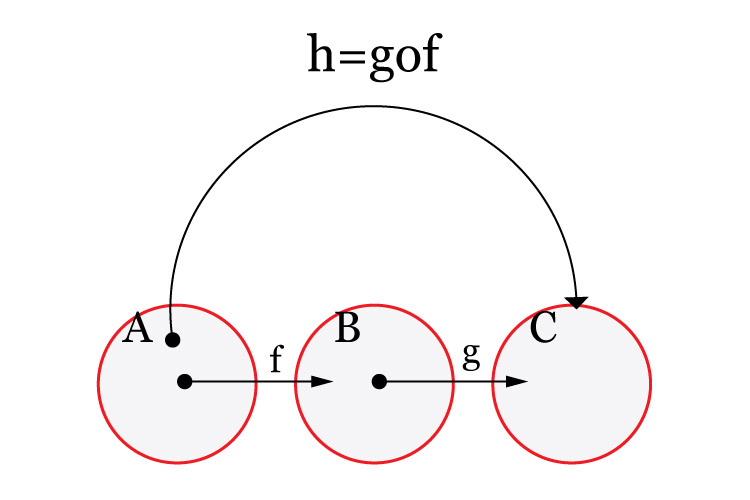
Não entendo só uma coisa. Muitas vezes os autores falam que se temos A(f(x) em B(g(x) em C (h(x) eles colocam sempre que de A para C é gof e não fog. Faço a maior confusão. De A para C não seria fog? Alguém pode me explicar isso?
Muito bom. Mas seria de maior agrado se elucidasses a análise gráfica da composição de funções.
Creio que a letra a do exemplo esteja errada. Não seria f (12)?
Corrigido Rodrigo, obrigado pela colaboração!